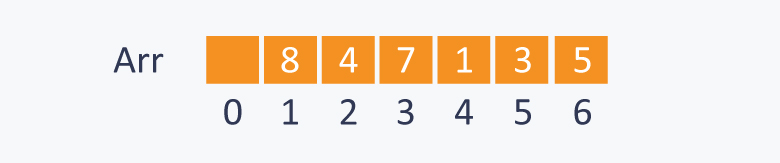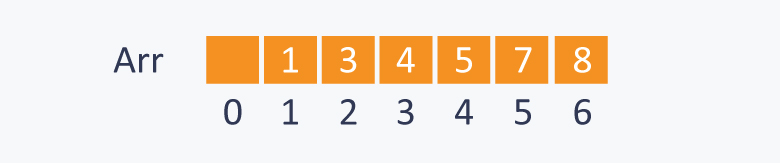数据结构

Posted on 本文总阅读量次

Arrays

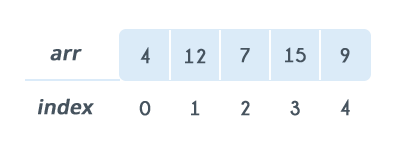
一维数组:

1
int arr[5] = {4, 12, 7, 15, 9};

1-D

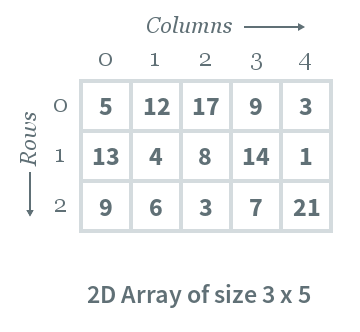
二维数组:N*M, 表示N行M列。

1
int arr[3][5] = {{5, 12, 17, 9, 3}, {13, 4, 8, 14, 1}, {9, 6, 3, 7, 21}};

2-D

Stacks

栈是只允许后进先出（LIFO）的动态数据结构。没有固定的大小。
栈只允许一端操作，出栈叫pop()，入栈叫push()。

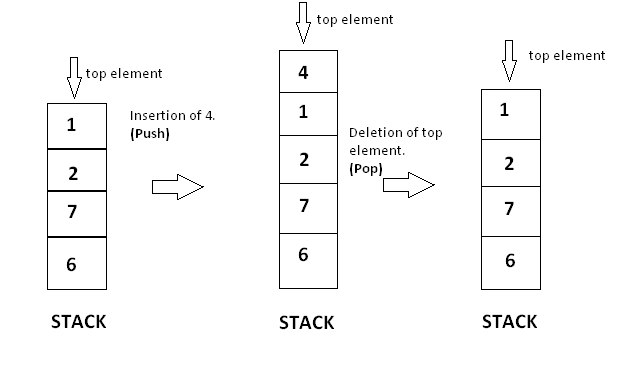
stack

push()

1
2
3
4
5
6
7
8
9
10
// x 是插入的元素，n是栈的最大容量
void push (int stack[ ] , int x , int n) {
 if ( top == n-1 ) {         //If the top position is the last of position in a stack, this means that the stack is full
    cout << “Stack is full.Overflow condition!” ;
    }
    else{
        top = top +1 ;            //Incrementing top position 
        stack[ top ] = x ;       //Inserting element on incremented position  
    }
}

pop()

1
2
3
4
5
6
7
8
9
10
11
12
void pop (int stack[ ] ,int n ) 
    {
        if( isEmpty ( ) )
        {
            cout << “Stack is empty. Underflow condition! ” << endl ;
        }
        else    
        {
             top = top - 1 ; //Decrementing top’s position will detach last element from stack            
        }
    }

Queues

队列是满足先进先出（FIFO）的数据结构。数据总是从尾端进入，从头部出去。

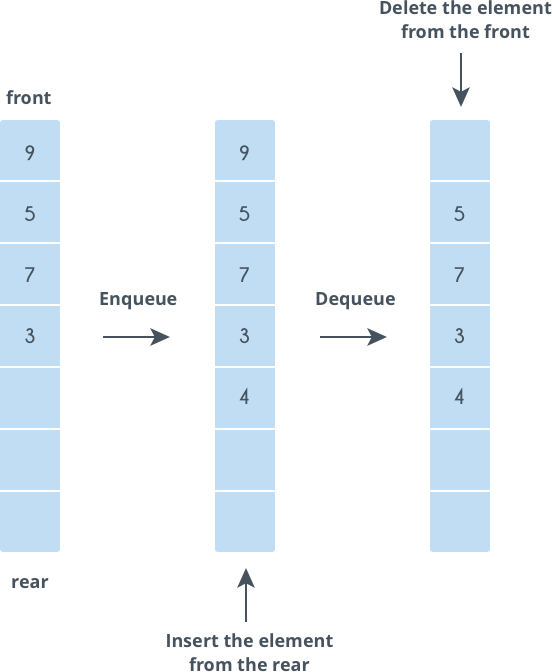
queue

enqueue()

1
2
3
4
5
6
7
8
void enqueue(int queue[], int element, int& rear, int arraySize) {
    if(rear == arraySize)            // Queue is full
            printf(“OverFlow\n”);
    else{
         queue[rear] = element;    // Add the element to the back
         rear++;
    }
}

dequeue()

1
2
3
4
5
6
7
8
void dequeue(int queue[], int& front, int rear) {
    if(front == rear)            // Queue is empty
        printf(“UnderFlow\n”);
    else {
        queue[front] = 0;        // Delete the front element
        front++;
    }
}

size()

1
2
3
int size(int front, int rear) {
    return (rear - front);
}

isEmpty()

1
2
3
bool isEmpty(int front, int rear) {
    return (front == rear);
}

双端队列，两端都可以进行出和进操作。
循环队列，解决空间浪费问题。

循环队列

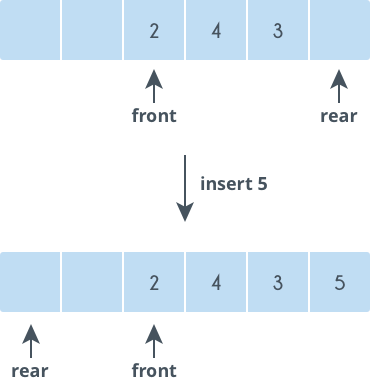
circle

enqueue

1
2
3
4
5
6
7
8
9
10
//使用count纪录队列的元素个数
void enqueue(int queue[], int element, int& rear, int arraySize, int count) {
    if(count == arraySize)            // Queue is full
            printf(“OverFlow\n”);
    else{
        queue[rear] = element;
        rear = (rear + 1)%arraySize;
        count = count + 1;
    }
}

dequeue

1
2
3
4
5
6
7
8
9
void dequeue(int queue[], int& front, int count) {
    if(count == 0)            // Queue is empty
        printf(“UnderFlow\n”);
    else {
        queue[front] = 0;        // Delete the front element
        front = (front + 1)%arraySize;
        count = count - 1;
    }
}

Hash Tables

哈希（散列）是一种能够在相似的元素集合中找到唯一标示的元素的技术。
使用哈希函数，将大的关键字转换成小的关键字，然后将值通过关键字存储在特定的数据结构中，叫做哈希表。
理想情况下：O(1)

哈希2步走：

  1. 元素通过哈希函数，转换成哈希表的索引。
  2. 将元素存储在索引对应的哈希表中。
    1
    2
    hash = hashfunc(key)
    index = hash % array_size

好的哈希函数：

  • 容易计算。
  • 分布均匀，避免堆积。
  • 更少的哈希冲突。

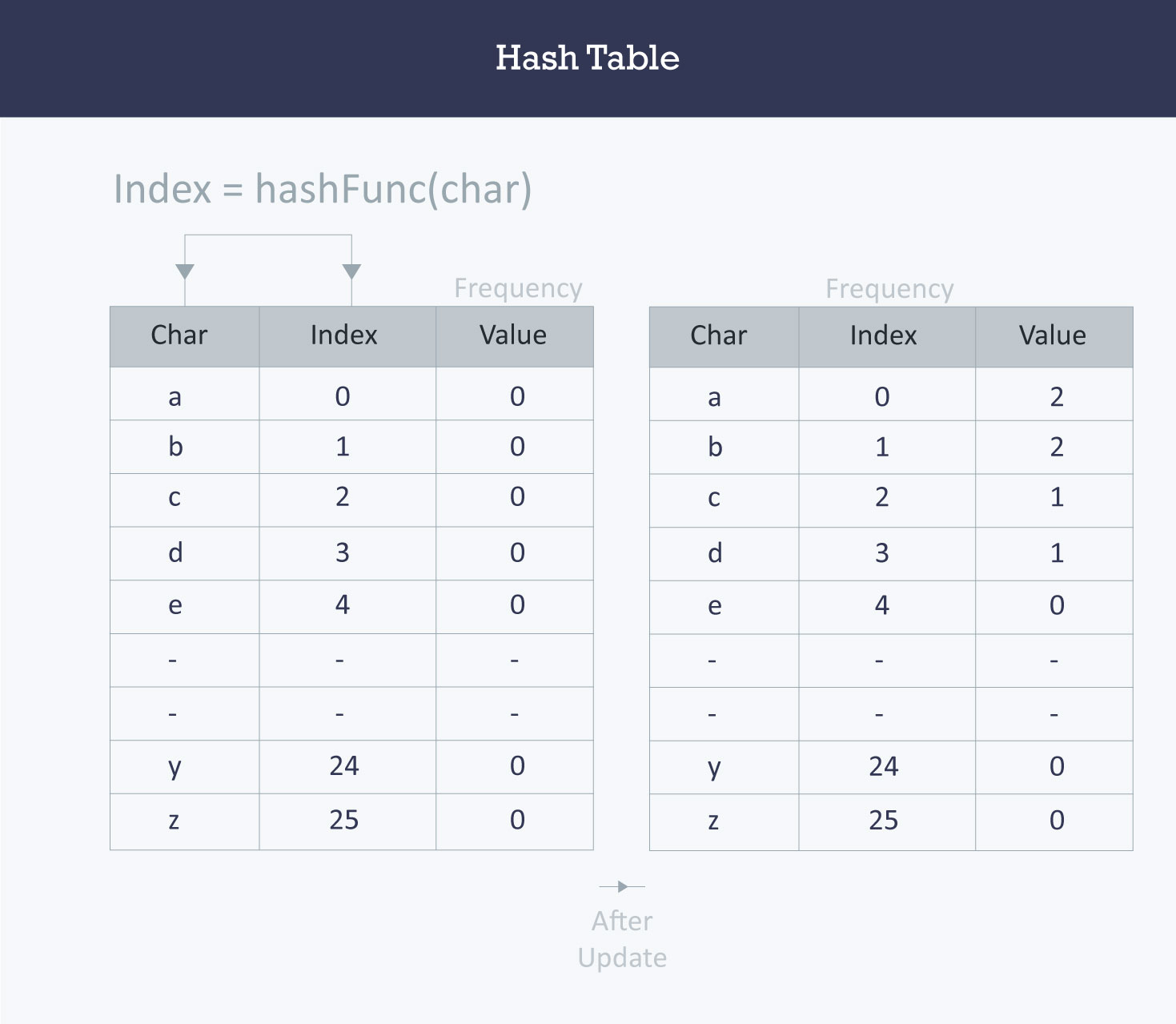
example:统计字符串中各个字符的频率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int Frequency[26];
    int hashFunc(char c)
    {
        return (c - ‘a’);
    }
    void countFre(string S)
    {
        for(int i = 0;i < S.length();++i)
        {
            int index = hashFunc(S[i]);
            Frequency[index]++;
        }
        for(int i = 0;i < 26;++i)
            cout << (char)(i+’a’) << ‘ ‘ << Frequency[i] << endl;
    }

hash-table

解决哈希冲突

分离链表发
哈希表的每一个元素，都是一张链表。当发生哈希冲突时，将它们同时放在链表里。

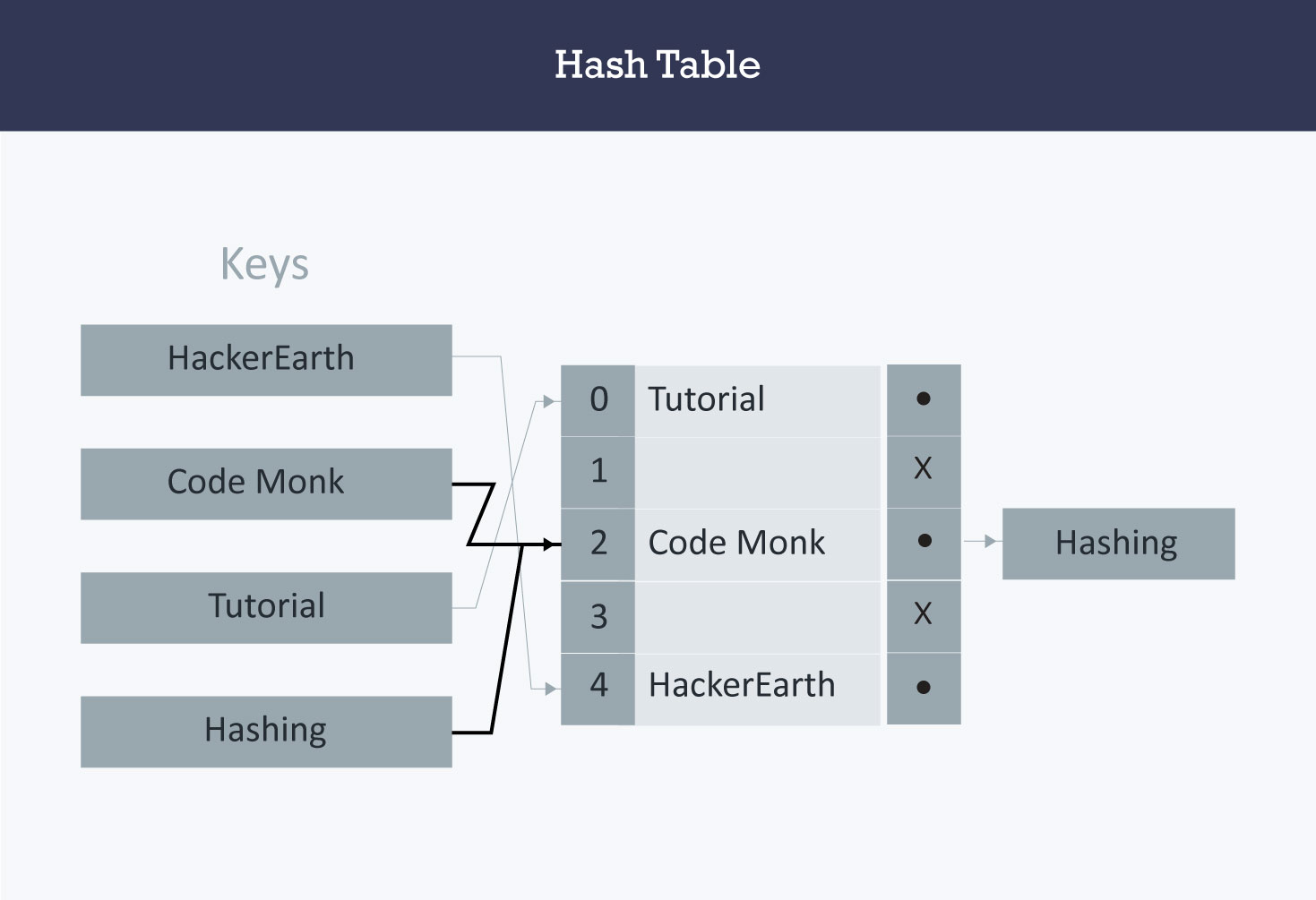
hash-collision

定义一个哈希链表

1
2
vector <string> hashTable[20];
    int hashTableSize=20;

insert

1
2
3
4
5
6
7
void insert(string s)
    {
                // Compute the index using Hash Function
        int index = hashFunc(s);
        // Insert the element in the linked list at the particular index
        hashTable[index].push_back(s);
    }

search

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void search(string s)
    {
        //Compute the index by using the hash function
        int index = hashFunc(s);
        //Search the linked list at that specific index
        for(int i = 0;i < hashTable[index].size();i++)
        {
            if(hashTable[index][i] == s)
            {
                cout << s << " is found!" << endl;
                return;
            }
        }
        cout << s << " is not found!" << endl;
    }

邻接地址法（开地址法）

如果当前地址没有元素，就存放。如果已经有了，就去向后找。

1
2
3
4
5
6
7
//线性探测
index = index % hashTableSize
index = (index + 1) % hashTableSize
index = (index + 2) % hashTableSize
index = (index + 3) % hashTableSize
and so on…

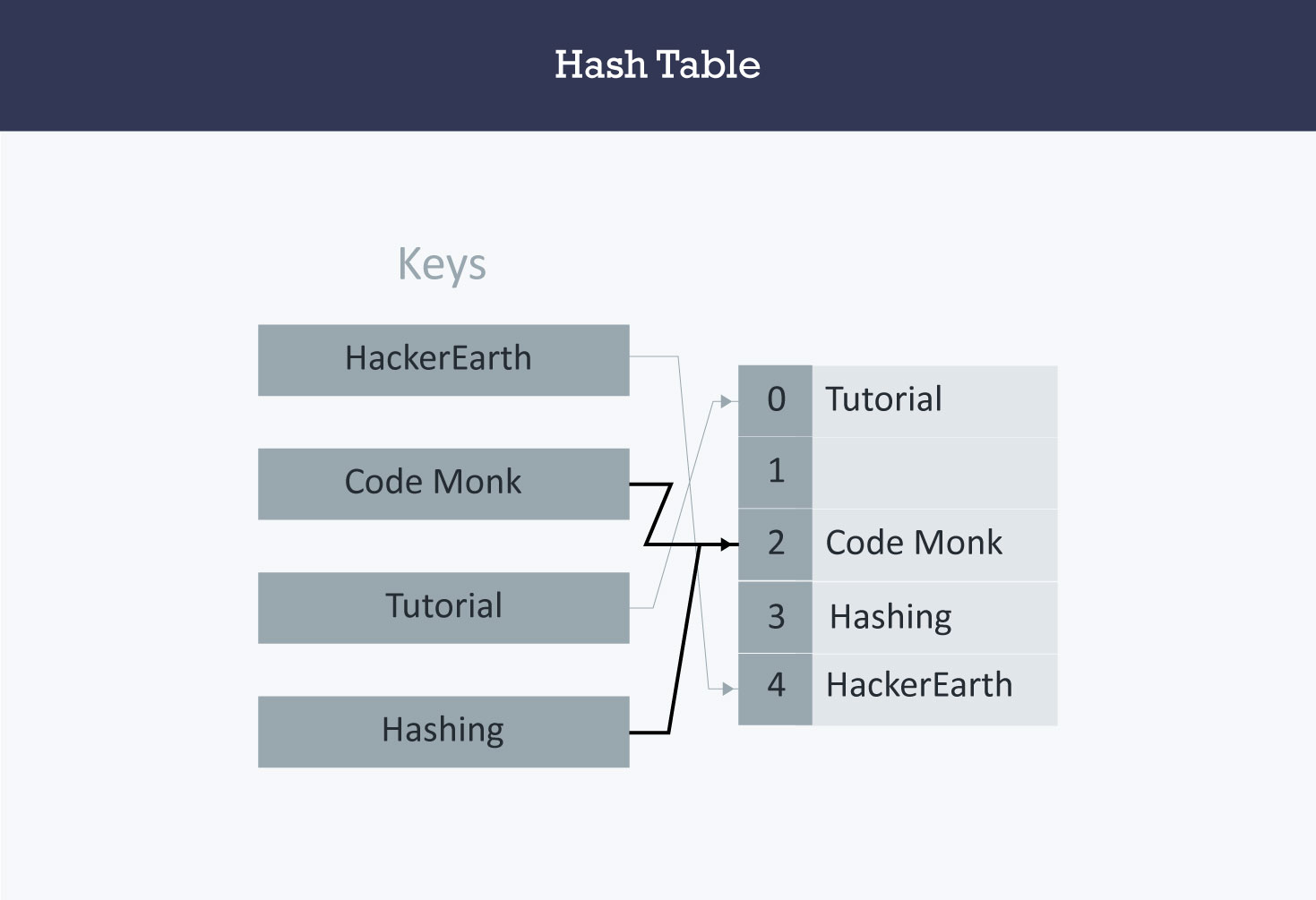
hash-near

定义哈希表

1
2
string hashTable[21];
int hashTableSize = 21;

insert

1
2
3
4
5
6
7
8
9
void insert(string s)
    {
        //Compute the index using the hash function
        int index = hashFunc(s);
        //Search for an unused slot and if the index will exceed the hashTableSize then roll back
        while(hashTable[index] != "")
            index = (index + 1) % hashTableSize;
        hashTable[index] = s;
    }

search

1
2
3
4
5
6
7
8
9
10
11
12
13
void search(string s)
   {
       //Compute the index using the hash function
       int index = hashFunc(s);
        //Search for an unused slot and if the index will exceed the hashTableSize then roll back
       while(hashTable[index] != s and hashTable[index] != "")
           index = (index + 1) % hashTableSize;
       //Check if the element is present in the hash table
       if(hashTable[index] == s)
           cout << s << " is found!" << endl;
       else
           cout << s << " is not found!" << endl;
   }

1
2
3
4
5
//二次探测
index = index % hashTableSize
index = (index + 12) % hashTableSize
index = (index + 22) % hashTableSize
index = (index + 32) % hashTableSize

哈希表应用：

  • 关联数组
  • 数据库索引
  • 缓存

Linked List

单链表定义：

1
2
3
4
struct LinkedList{
    int data;
    struct LinkedList *next;
 };

linked-list
link

创建node

1
2
3
4
5
6
7
8
 typedef struct LinkedList *node; //Define node as pointer of data type struct LinkedList
node createNode(){
    node temp; // declare a node
    temp = (node)malloc(sizeof(struct LinkedList)); // allocate memory using malloc()
    temp->next = NULL;// make next point to NULL
    return temp;//return the new node
}

addNode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
node addNode(node head, int value){
    node temp,p;// declare two nodes temp and p
    temp = createNode();//createNode will return a new node with data = value and next pointing to NULL.
    temp->data = value; // add element's value to data part of node
    if(head == NULL){
        head = temp;     //when linked list is empty
    }
    else{
        p  = head;//assign head to p 
        while(p->next != NULL){
            p = p->next;//traverse the list until p is the last node.The last node always points to NULL.
        }
        p->next = temp;//Point the previous last node to the new node created.
    }
    return head;
}

Trees

Binary/N-ary Trees

二叉树由多个节点组成，每一个节点满足：

  1. 节点保存数据
  2. 左指针指向左节点
  3. 右指针指向右节点

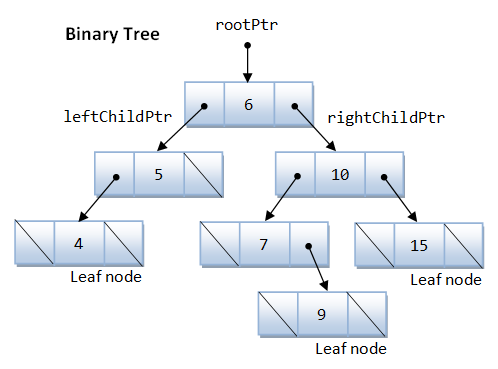
binary-tree

  • Root: Top node in a tree
  • Child: Nodes that are next to each other and connected downwards
  • Parent: Converse notion of child
  • Siblings: Nodes with the same parent
  • Descendant: Node reachable by repeated proceeding from parent to child
  • Ancestor: Node reachable by repeated proceeding from child to parent.
  • Leaf: Node with no children
  • Internal node: Node with at least one child
  • External node: Node with no children

定义：

1
2
3
4
5
6
struct node
    {
         int data;                 //Data element
         struct node * left;          //Pointer to left node
         struct node * right;         //Pointer to right node
    };

创建节点

1
2
3
4
5
6
7
struct node * newnode(int element)
    {
        struct node * temp=(node * )malloc(sizeof(node));
        temp->data=element;
        temp->left=temp->right=NULL;
        return temp;
    }

计算树的高度:O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int maxDepth(struct node* node) 
    {
        if (node==NULL) 
            return 0;
        else
        {
             /* compute the depth of each subtree */
              int lDepth = maxDepth(node->left);
              int rDepth = maxDepth(node->right);
              /* use the larger one */
              if (lDepth > rDepth) 
                    return(lDepth+1);
              else 
                   return(rDepth+1);
       }
    }

树的应用：

  • 处理分层数据
  • 搜索
  • 排序集合
  • 路由

Binary Search Tree

二叉搜索树是满足以下条件的二叉树。

  • 所有节点的左子树的节点都<=当前节点。
  • 所有节点的右子树的节点都>=当前节点。

bst

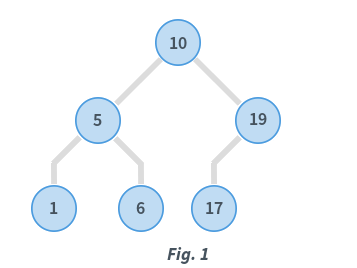
遍历树的三种方式：（以root节点的顺序命名）

先序遍历: root->left->right

1
2
3
4
5
6
7
8
9
void preorder(struct node*root)
   {
       if(root)
       {
           printf("%d ",root->data);    //Printf root->data
           preorder(root->left);    //Go to left subtree
           preorder(root->right);     //Go to right subtree
       }
   }

后序遍历: left->right->root

1
2
3
4
5
6
7
8
9
void postorder(struct node*root)
    {
        if(root)
        {
            postorder(root->left);    //Go to left sub tree
            postorder(root->right);     //Go to right sub tree
            printf("%d ",root->data);    //Printf root->data
        }
    }

中序遍历：left->root->right

1
2
3
4
5
6
7
8
9
void inorder(struct node*root)
    {
        if(root)
        {
            inorder(root->left);    //Go to left subtree
            printf("%d ",root->data);    //Printf root->data
            inorder(root->right);     //Go to right subtree
        }
    }

树的中序遍历产生有序的遍历结合

插入BST

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct node* insert(struct node* root, int data)
    {
        if (root == NULL)    //If the tree is empty, return a new,single node
            return newNode(data);
        else
        {
            //Otherwise, recur down the tree 
            if (data <= root->data)
                root->left  = insert(root->left, data);
            else
                root->right = insert(root->right, data);
            //return the (unchanged) root pointer 
            return root;
        }
    }

Heaps/Priority Queues

大堆：任何父节点的值都大于其子孙节点。
假设ROOT映射到数组下标1。
子节点可以通过(h - 1) * 2 和 (h - 1) * 2 + 1 映射到数组下标。h是父节点下标。
heap

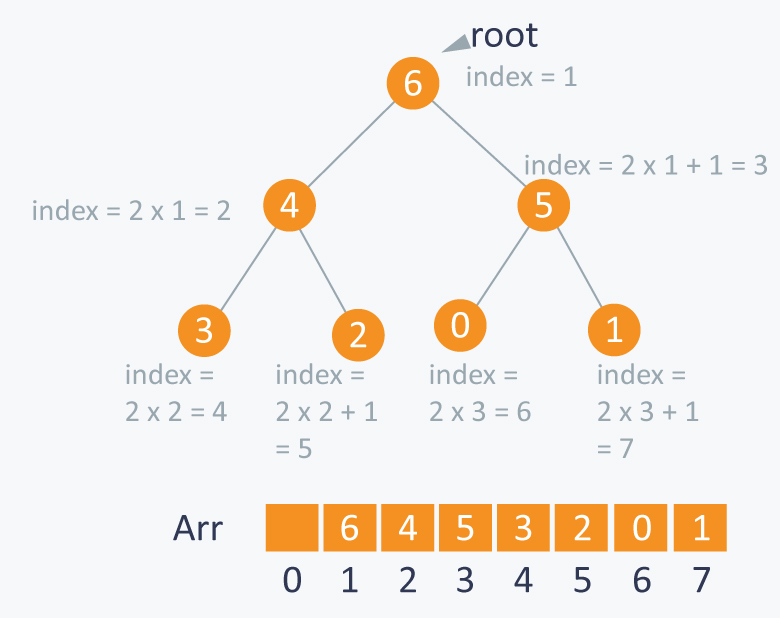
将下标是i的节点大堆化，N是数组大小。O(logN)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void max_heapify (int Arr[ ], int i, int N)
    {
        int left = 2*i                   //left child
        int right = 2*i +1           //right child
        if(left<= N and Arr[left] > Arr[i] )
              largest = left;
        else
             largest = i;
        if(right <= N and Arr[right] > Arr[largest] )
            largest = right;
        if(largest != i )
        {
            swap (Arr[i] , Arr[largest]);
            max_heapify (Arr, largest,N);
        } 
     }

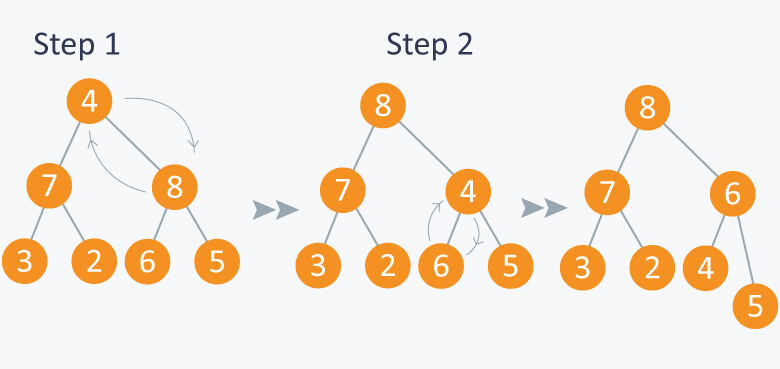
heapify

从数组构建大堆：因为arr[n/2+1]~arr[n]是叶子节点。O(N)

1
2
3
4
5
6
7
8
void build_maxheap (int Arr[ ])
    {
        //从下到上遍历
        for(int i = N/2 ; i >= 1 ; i-- )
        {
            max_heapify (Arr, i) ;
        }
    }

堆排序 O(Nlog(N))`

排序过程：

  1. 构建大堆树
  2. 将root(当前最大节点）与数组最后一个节点交换。这时，最后一个节点已经有序。
  3. 数组大小减1，重复执行1，2步骤。
1
2
3
4
5
6
7
8
9
10
11
void heap_sort(int Arr[ ])
    {
        int heap_size = N;
        build_maxheap(Arr);//构建堆
        for(int i = N; i>=2 ; i-- )
        {
            swap(Arr[ 1 ], Arr[ i ]);//把最大的移到末尾
            heap_size = heap_size-1;
            max_heapify(Arr, 1, heap_size);//根节点堆化
        }
    }

图解：

arr
step
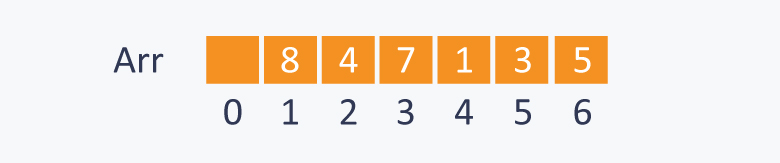
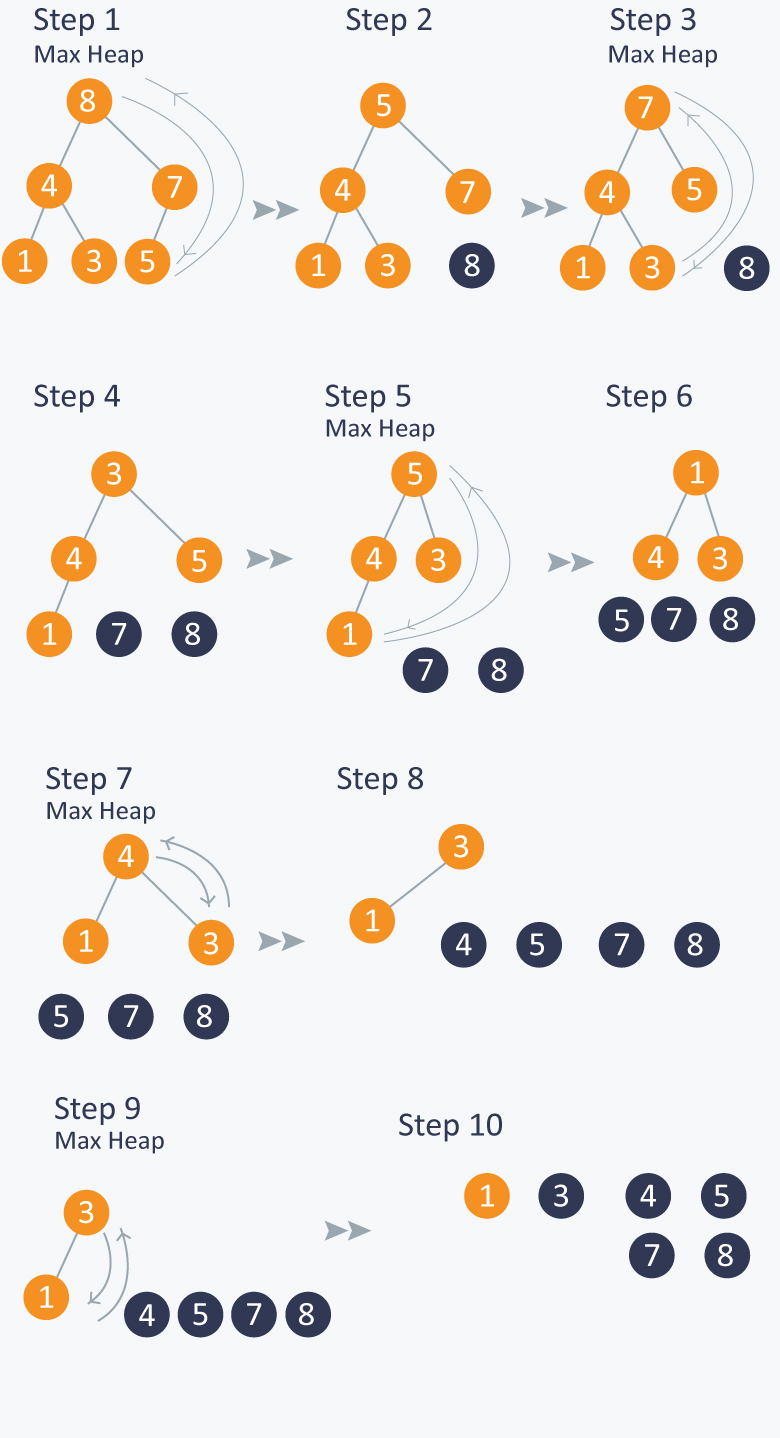
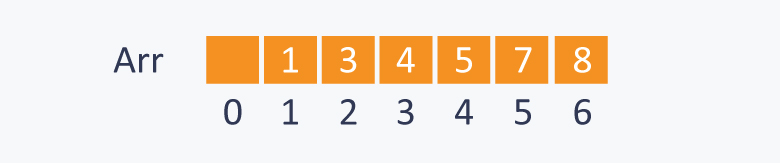
result

优先级队列

优先级队列每次都要求优先级最高的先出站。我们可以创建一个对应的堆。
将对最大值放到根节点，然后出队列。最后一个元素放到根节idan，然后通过上面的max_heapify(Arr, 1, heap_size)，调整堆。
出队列的操作：O(logN)

Trie(Keyword Tree)

字符串处理是重要和常见的话题。
如：

  • 搜索引擎
  • 基因分析
  • 数据分析

Tries是基于字符串前缀的数据结构。

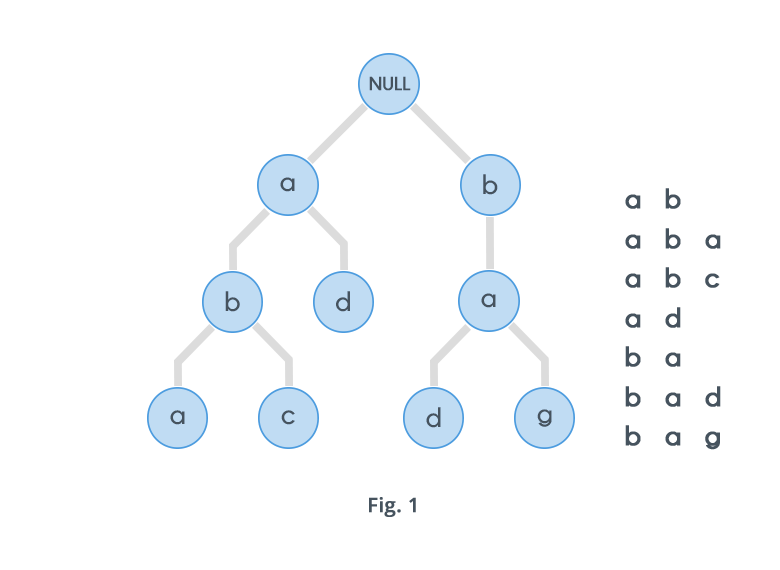
tries

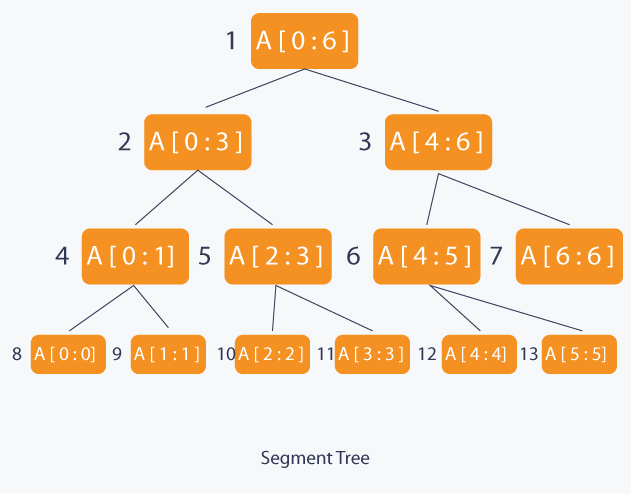
Segment Trees

分段树用于范围查找，如计算数组L到R之间所有元素的和。
比如：
一个N个元素的数组:

  • 根节点A[0：N-1]
  • 叶子节点A[i]，0<=i<N
  • 中间节点A[i,j], 0<=i<j<N
  • 树的高度log2N,树节点总数2*N-1

segement-tree

Disjoin Data

并查集
如：有一个数组

arr

执行两种操作：

  1. Find(A, B) : 检查arr[A]==arr[B]?
  2. Union(A, B): 将arr[B]的值赋给arr[A]

执行以下操作：
Union(2,1)
Union(4,3)
Union(8,4)
Union(9,3)
Union(6,5)

将分成5个集合

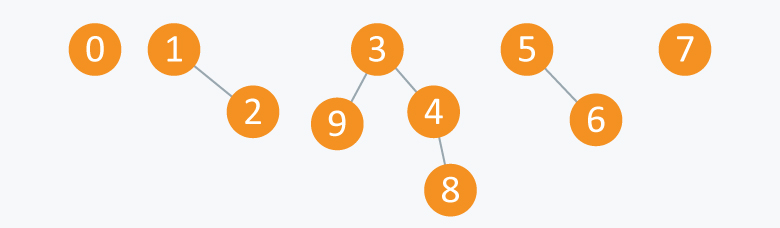
union

数组变成

arr

初始化：有N个集合，每个集合一个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void initialize( int Arr[ ], int N)
   {
       for(int i = 0;i<N;i++)
       Arr[ i ] = i ;
   }
   //returns true if A and B are connected, else returns false 
    bool find( int Arr[ ], int A, int B)                           
   {
   if(Arr[ A ] == Arr[ B ])
   return true;
   else
   return false;   
   }
   //change all entries from arr[ A ] to arr[ B ].
   void union(int Arr[ ], int N, int A, int B)
   {
       int TEMP = Arr[ A ];
   for(int i = 0; i < N;i++)
       {
       if(Arr[ i ] == TEMP)
       Arr[ i ] = Arr[ B ]; 
       }
   }
数据结构
© 2017 Hello World All Rights Reserved. 本站访客数人次 本站总访问量次
Theme by hiero