算法基础

Posted on 五月 3, 2017 本文总阅读量次

Linear Search

如果我们要查找数组中等于5的值，需要遍历数组。时间复杂度 $ O(N) $

Binary Serach

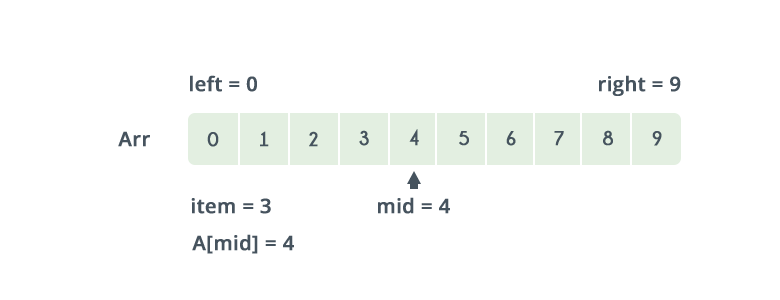
二分查找，前提是集合有序。

1
2
3

Low = 0
High = n-1
Mid = (Low + High)/2

首先找到中间值比较，如果大于当前值，就往低处找，否则往高处找。直道当前值等于中间值。
时间复杂度：$ \log_2 N $

int binarySearch(int low,int high,int key)
{
   while(low<=high)
   {
     int mid=(low+high)/2;
     if(a[mid]<key)
     {
         low=mid+1;
     }
     else if(a[mid]>key)
     {
         high=mid-1;
     }
     else
     {
         return mid;
     }
   }
   return -1;                //key not found
 }

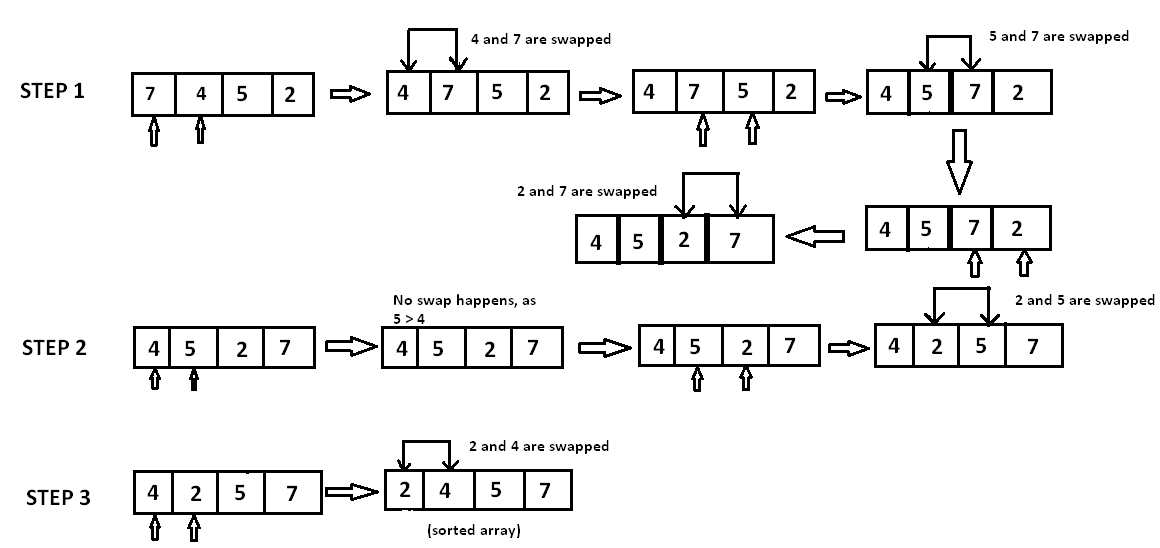
Bubble Sort

冒泡排序: 反复比较相邻的两个元素，如果顺序不对，就互相交换，直到集合有序。
每经过一趟排序，最大的值会冒到最后的位置。
时间复杂度：$ O(N^2) $

void bubble_sort( int A[ ], int n ) {
    int temp;
    for(int k = 0; k< n-1; k++) {
        // (n-k-1) is for ignoring comparisons of elements which have already been compared in earlier iterations
        for(int i = 0; i < n-k-1; i++) {
            if(A[ i ] > A[ i+1] ) {
                // here swapping of positions is being done.
                temp = A[ i ];
                A[ i ] = A[ i+1 ];
                A[ i + 1] = temp;
            }
        }
    }
}

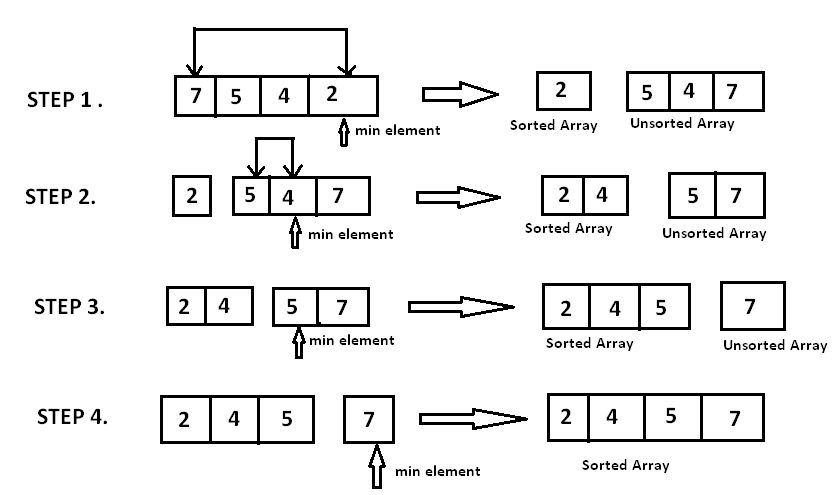
Selection Sort

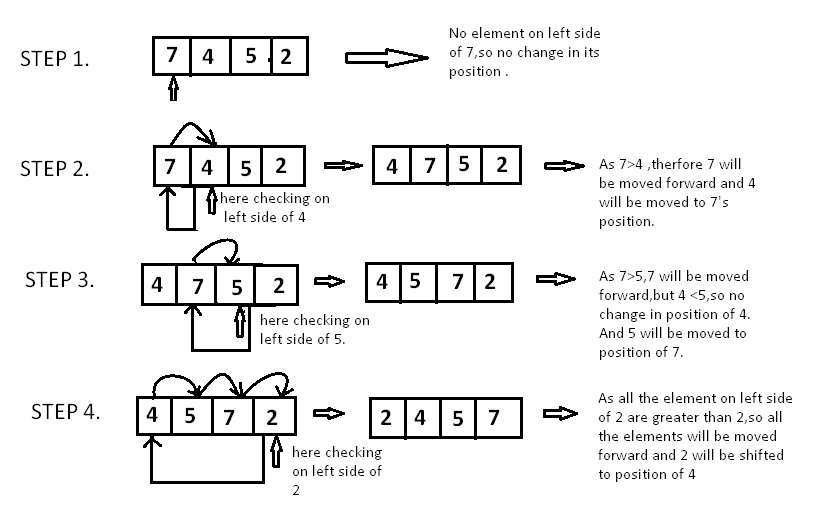
选择排序：找到当前最大的元素，放到正确的位置上，使集合有序。
时间复杂度：$ O(N^2) $

void selection_sort (int A[ ], int n) {
        // temporary variable to store the position of minimum element
        int minimum;        
        // reduces the effective size of the array by one in  each iteration.
        for(int i = 0; i < n-1 ; i++)  {
           // assuming the first element to be the minimum of the unsorted array .
             minimum = i ;
          // gives the effective size of the unsorted  array .
            for(int j = i+1; j < n ; j++ ) {
                if(A[ j ] < A[ minimum ])  {                //finds the minimum element
                minimum = j ;
                }
             }
          // putting minimum element on its proper position.
          swap ( A[ minimum ], A[ i ]) ; 
        }
   }

Insertion Sort

插入排序:假设开始只有一个元素，集合是有序的，取之后的元素，遍历已经有序集合，找到当前元素的正确位置，并插入。

时间按复杂度：$ O(N^2) $

void insertion_sort ( int A[ ] , int n) 
{
     for( int i = 0 ;i < n ; i++ ) {
    /*storing current element whose left side is checked for its 
             correct position .*/
      int temp = A[ i ];    
      int j = i;
       /* check whether the adjacent element in left side is greater or
            less than the current element. */
          while(  j > 0  && temp < A[ j -1]) {
           // moving the left side element to one position forward.
                A[ j ] = A[ j-1];   
                j= j - 1;
           }
         // moving current element to its  correct position.
           A[ j ] = temp;       
     }  
}

Merge Sort

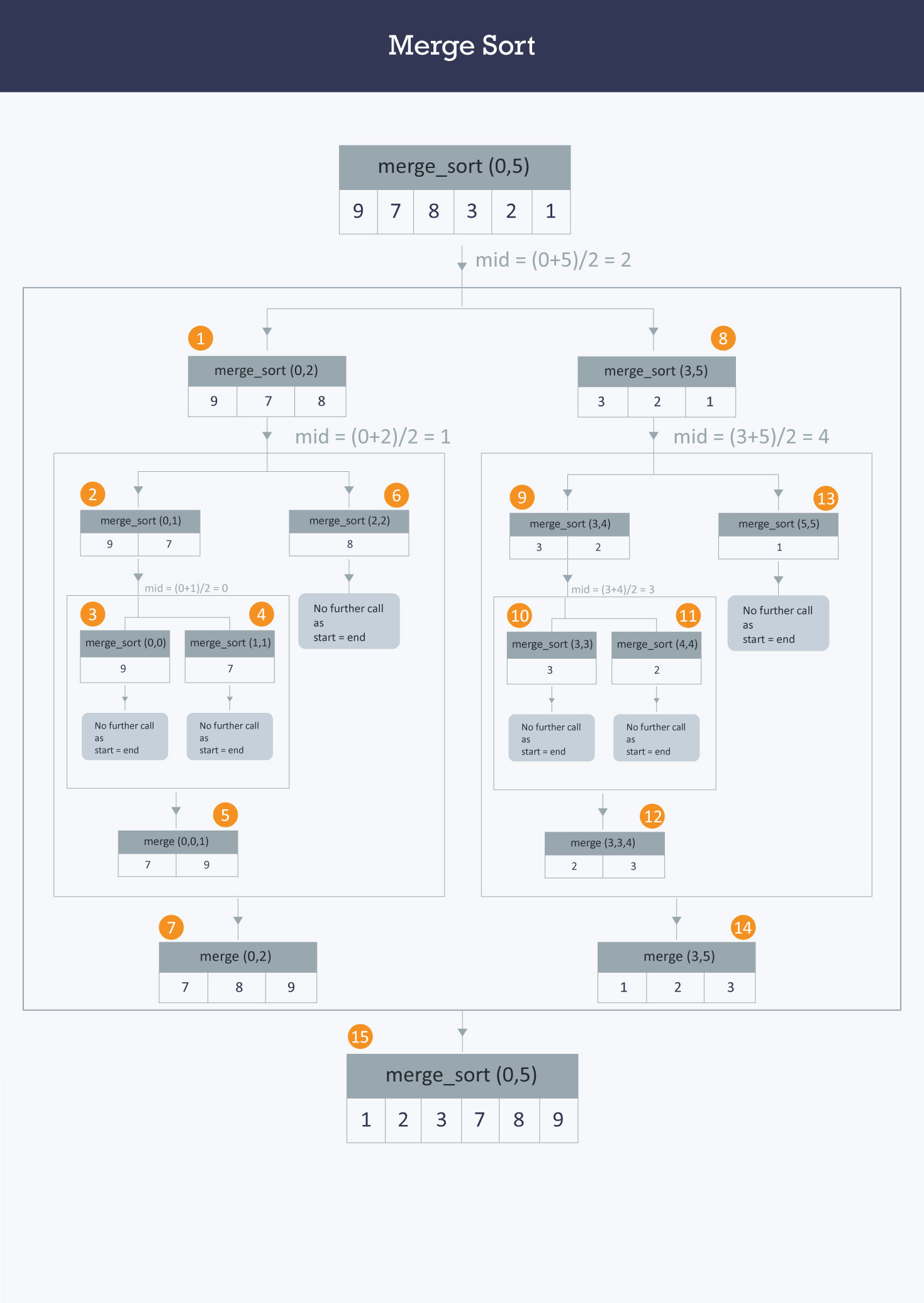
归并排序 ：是基于分治算法的，将当前集合分成几个更小的子集，直到子集只包含一个元素，那么自己是有序的，然后合并自己，直到整个集合有序。
时间复杂度：$ O(NlogN) $

void merge(int A[ ] , int start, int mid, int end) {
 //stores the starting position of both parts in temporary variables.
int p = start ,q = mid+1;
int Arr[end-start+1] , k=0;
for(int i = start ;i <= end ;i++) {
    if(p > mid)      //checks if first part comes to an end or not .
       Arr[ k++ ] = A[ q++] ;
   else if ( q > end)   //checks if second part comes to an end or not
       Arr[ k++ ] = A[ p++ ];
   else if( A[ p ] < A[ q ])     //checks which part has smaller element.
      Arr[ k++ ] = A[ p++ ];
   else
      Arr[ k++ ] = A[ q++];
 }
  for (int p=0 ; p< k ;p ++) {
   /* Now the real array has elements in sorted manner including both 
        parts.*/
     A[ start++ ] = Arr[ p ] ;                          
  }
}

void merge_sort (int A[ ] , int start , int end )
   {
           if( start < end ) {
           int mid = (start + end ) / 2 ;           // defines the current array in 2 parts .
           merge_sort (A, start , mid ) ;                 // sort the 1st part of array .
           merge_sort (A,mid+1 , end ) ;              // sort the 2nd part of array.
         // merge the both parts by comparing elements of both the parts.
          merge(A,start , mid , end );   
   }                    
}

Quick Sort

快排:基于分治算法。随机选择一个元素，将大于这个元素和小于这个元素分成两个集合，直到集合只有一个元素

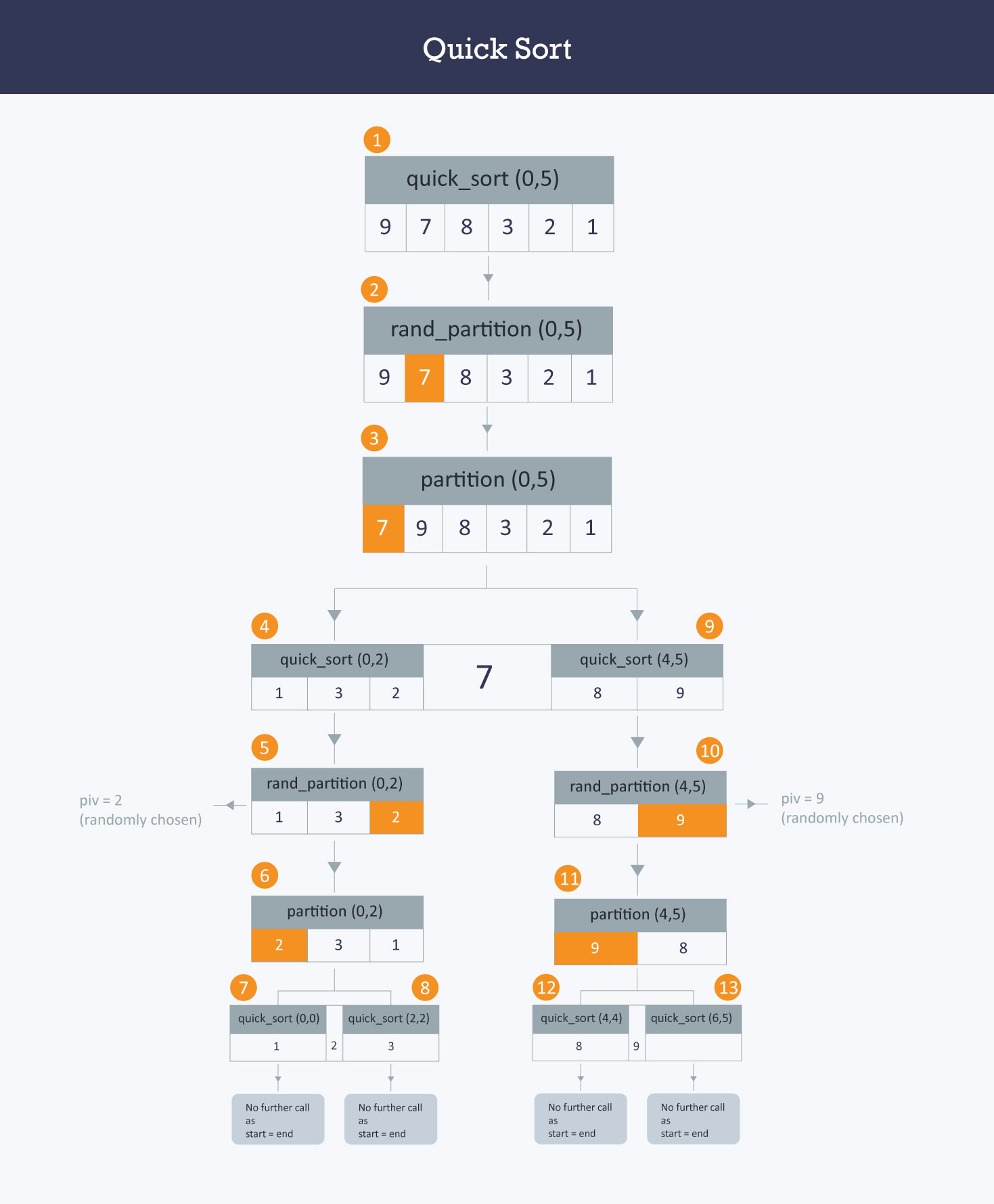
随机选择一个元素7，与第一个元素交换
将7作为基准

1<7 9="" 1,9,8,3,2,7="">7 1,7,8,3,2,9
2<7 8="" 1,2,8,3,7,9="">7 1,2,7,3,8,9
3<7 1,2,3,7,8,9

这时[1,2,3] 7 [8,9]

随机选择2作为基点,与第一个交换2,1,3

3>1
1<2 1,2,3
这时1[2]3 有序
随机选择9作为基点，与第一个交换9,8
8<9 8,9
这时有序

int rand_partition ( int A[ ] , int start , int end ) {
    //chooses position of pivot randomly by using rand() function .
     int random = start + rand( )%(end-start +1 ) ;
      swap ( A[random] , A[start]) ;        //swap pivot with 1st element.
     return partition(A,start ,end) ;       //call the above partition function
}

int partition ( int A[],int start ,int end) {
    int i = start + 1;
    int piv = A[start] ;            //make the first element as pivot element.
    for(int j =start + 1; j <= end ; j++ )  {
    /*rearrange the array by putting elements which are less than pivot
       on one side and which are greater that on other. */
          if ( A[ j ] < piv) {
                 swap (A[ i ],A [ j ]);
            i += 1;
        }
   }
   swap ( A[ start ] ,A[ i-1 ] ) ;  //put the pivot element in its proper place.
   return i-1;                      //return the position of the pivot
}

void quick_sort ( int A[ ] ,int start , int end ) {
   if( start < end ) {
        //stores the position of pivot element
         int piv_pos = partition (A,start , end ) ;     
         quick_sort (A,start , piv_pos -1);    //sorts the left side of pivot.
         quick_sort ( A,piv_pos +1 , end) ; //sorts the right side of pivot.
   }
}

Greedy Algorithms

面对不同的问题，需要不同的算法。
常用的算法：

分治算法

随机算法

贪心算法(确切地说应该是一种技术)

动态规划

贪婪算法 : 总是选择当前最优解。不会反悔已经做得决定。

优点：容易找到解决问题的方法，容易计算时间复杂度。
缺点：很难证明结果的正确性。

如：
有一个数组A，A中每一个数字代表任务花费的时间，计算T时间内最多能做几件事。

将数组A按升序排序。
遍历数组，累加每一个任务花费的时间，直到大于T。